FreeVue-Hug

문제

1부터 자연수를 차례로 더하여 구해진 값을 삼각수라고 합니다.

삼각수: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...

 1: 1
 3: 1, 3
 6: 1, 2, 3, 6
10: 1, 2, 5, 10
15: 1, 3, 5, 15
21: 1, 3, 7, 21
28: 1, 2, 4, 7, 14, 28

위는 삼각수의 약수입니다.

n개 이상의 약수를 갖는 가장 작은 삼각수를 구하시오.

풀이

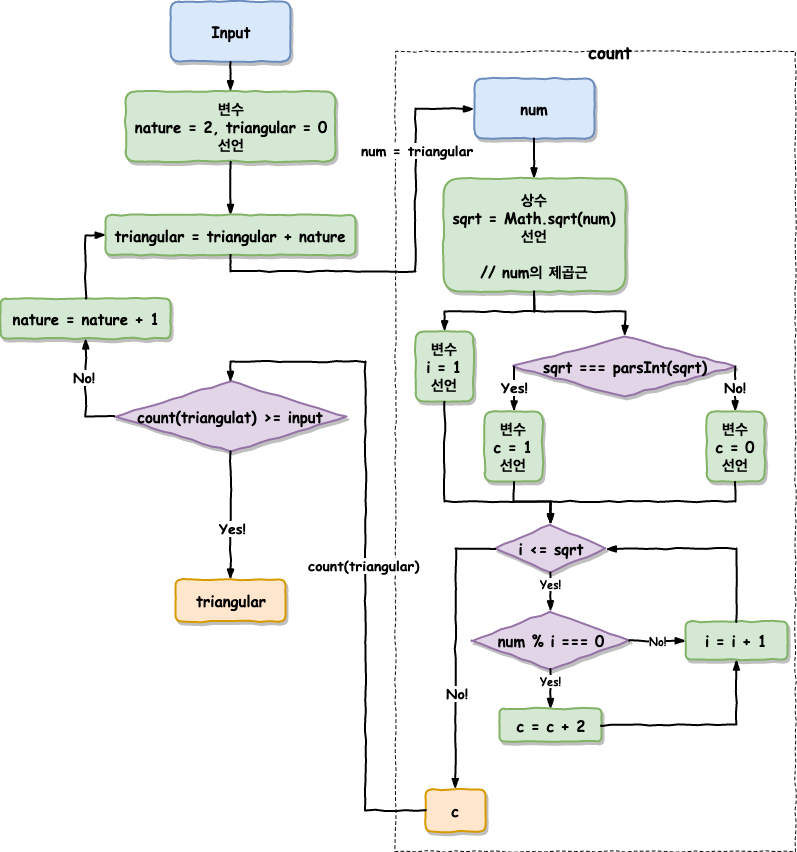
const output = (input) => {
  const count = (num) => {
    // 약수의 갯수를 구할 함수
    const sqrt = Math.sqrt(num) // num의 제곱근

    // 약수를 담을 i와 갯수를 담을 c를 선언
    //
    // 제곱근의 값이 정수일 경우 갯수는 1부터 시작한다.
    let i = 1
    let c = sqrt === parseInt(sqrt) ? 1 : 0

    // 약수들을 구할 반복문
    while (i <= sqrt) {
      // 약수일 경우 카운트를 올린다.
      //
      // num이 아닌 제곱근까지 비교를 하기 때문에 2씩 더한다.
      if (num % i === 0) c += 2

      i++
    }

    // 갯수를 출력
    return c
  }

  // 삼각수와 1씩 증가할 자연수를 선언
  let nature = 1
  let triangular = 0

  // 무한반복
  while (true) {
    // 삼각수에 자연수를 더해 삼각수를 구한다.
    triangular += nature

    // 삼각수의 약수의 갯수와 input을 비교하고 조건에 따라 반복을 중지한다.
    if (count(triangular) >= input) break

    // 자연수에 1을 더한다.
    nature++
  }

  // 삼각수를 출력
  return triangular
}

output(4) // 6
output(6) // 28
output(100) // 73920
output(500) // 76576500

구조

결과 이미지 1

[출처: http://euler.synap.co.kr/prob_detail.php?id=12]

알고리즘 풀이

문제

풀이

구조